Fourier transforms of measures

Fourier transforms play an important role in the dimension theory of fractals, as well as describing many other geometric properties. The Fourier dimension of a measure captures the rate at which the Fourier transform decays at infinity and the Fourier dimension of a set is the supreum of the Fourier dimension of measures it supports. A non-trivial and highly useful fact to keep in mind is that the Fourier dimension of a set never exceeds the Hausdorff dimension. Sets for which the Fourier transform and Hausdorff dimension coincide are known as Salem sets. Salem sets abound in random settings, through pioneering work of Kahane and others, however, (non-trivial) deterministic Salem sets are much rarer. An old question of Kahane asked if the graph of Brownian motion was almost surely a Salem set. By establishing a Fourier analytic slicing theorem, we proved that the graph of any function on the reals never exceeds 1. This answers Kahane's question in the negative, since the Hausdorff dimension of the graph of Brownian motion is almost surely 3/2. Note that our solution is geometric, not stochastic:

► On Fourier analytic properties of graphs (with T. Orponen & T. Sahlsten), arXiv
        International Mathematics Research Notices (IMRN), (2014), 2730-2745.

The natural follow up (stochastic) qustion was to determine what the (almost sure) Fourier dimension of the graph of Brownian actually is. We proved that is 1, the maximum value possible:

► On the Fourier analytic structure of the Brownian graph (with T. Sahlsten), arXiv
        Analysis & PDE, 11, (2018), 115-132.

Other work on Fourier transforms includes:

► The Fourier spectrum and sumset type problems, arXiv
        Mathematische Annalen (to appear).

► L^p averages of the Fourier transform in finite fields, arXiv
        submitted.

► Obtaining the Fourier spectrum via Fourier coefficients (with M. Carnovale and A. E. de Orellana), arXiv
        submitted.

► A Fourier analytic approach to exceptional set estimates for orthogonal projections (with A. E. de Orellana), arXiv
        submitted.

► Fourier decay of product measures, arXiv
        submitted.

► On the Fourier dimension of (d,k)-sets and Kakeya sets with restricted directions (with T. Harris and N. Kroon), arXiv
        Mathematische Zeitschrift, 301, (2022), 2497-2508.

► Improved bounds on the dimensions of sets that avoid approximate arithmetic progressions (with P. Shmerkin & A. Yavicoli), arXiv
        Journal of Fourier Analysis and Applications, 27, (2021).

I gave a talk about my work with Tuomas Sahlsten at Fractal Geometry, Hyperbolic Dynamics and Thermodynamical Formalism at ICERM (Brown University) in March 2016. Here is the video and here are the slides.

I gave a talk about my work with Orponen and Sahlsten on Kahane's problem at an ETDS meeting in Jagiellonian University in 2014. Here are the slides.



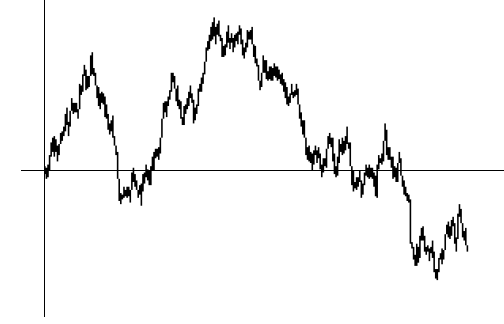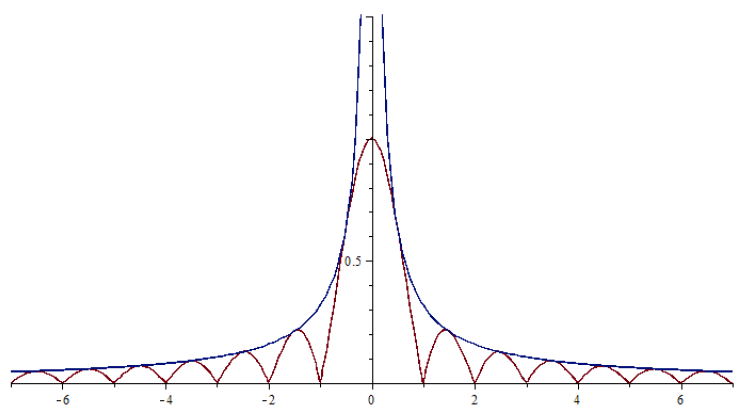
Left: the Fourier transform of Lebesgue measure restricted to the unit interval together with a decay envelope. Right: (one realisation of) the graph of Brownian motion.