Conformal dynamics

Kleinian groups are discrete groups of isometries acting on hyperbolic space (Fuchsian if the hyperbolic space is 2-dimensional). They act conformally on the boundary at infinity and give rise to beautiful fractal limit sets. Rational maps act conformally on the Riemann sphere (complex plane plus a point at infinity) and give rise to beautiful fractal Julia sets. I have studied fractal properties of both of these objects, as well as the Sullivan dictionary which seeks connection between the two settings. I've also worked on self-conformal sets. Some papers include:

► Assouad type dimensions of parabolic Julia sets (with L. Stuart), arXiv
        submitted.

► A new perspective on the Sullivan dictionary via Assouad type dimensions and spectra (with L. Stuart), arXiv
        Bulletin of the American Mathematical Society, 61, (2024), 103–118.

► Refined horoball counting and conformal measure for Kleinian group actions (with L. Stuart), arXiv
        Annales Fennici Mathematici, 48, (2023), 325–344.

► Intermediate dimensions of infinitely generated attractors (with A. Banaji), arXiv
        Transactions of the American Mathematical Society, 376, (2023), 2449-2479.

► The Assouad spectrum of Kleinian limit sets and Patterson-Sullivan measure (with L. Stuart), arXiv
        Geometriae Dedicata, 217, (2023), Paper No. 1, 32 pp.

► Regularity of Kleinian limit sets and Patterson-Sullivan measures, arXiv
        Transactions of the American Mathematical Society, 372, (2019), 4977-5009.

► Micromeasure distributions and applications for conformally generated fractals (with M. Pollicott), arXiv
        Mathematical Proceedings of the Cambridge Philosophical Society, 159, (2015), 547-566.

I gave a talk about my work with Liam Stuart on the Sullivan dictionary at the Seminaire Cristolien d'Analyse Multifractale, CNRS, France, 17 December 2020. Here is a video and here are the slides.



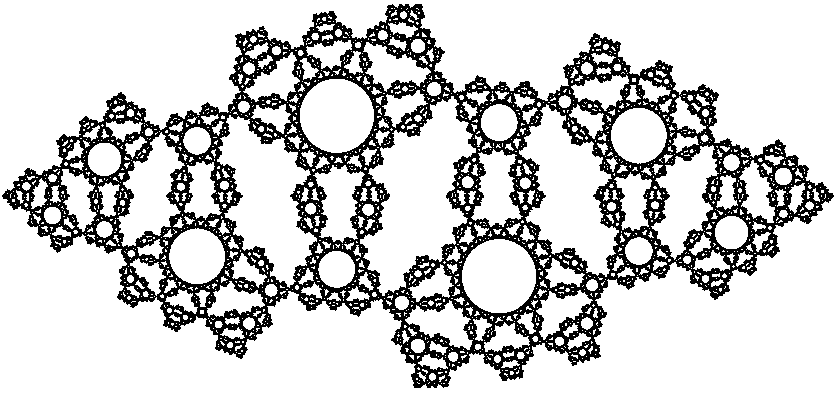On the left is the limit set of a Kleinian group and on the right is a Julia set of a parabolic rational map.