Dimension interpolation

One of the most beautiful and fundamental questions in fractal geometry is how to define the dimension of a fractal set or measure. There are many different ways to do this, each sensitive to a different geometric feature. Dimension interpolation is a new idea which seeks to understand the relationship between two given notions of dimension by viewing them as different facets of the same object: a continuum of dimensions varying from one to the other. There are three main ways to do this: the Assouad spectrum (introduced with Han Yu), intermediate dimensions (introduced with Kenneth Falconer and Tom Kempton) and the Fourier dimension spectrum (recently introduced). I wrote a survey paper on the general idea for the proceedings of Fractal Geometry and Stochastics VI, which is probably a good place to start:

► Interpolating between dimensions, arXiv
        Proceedings of Fractal Geometry and Stochastics VI, Birkhäuser, Progress in Probability, 2021.

The paper in which we introduced the Assouad spectrum is here:

► New dimension spectra: finer information on scaling and homogeneity (with H. Yu), arXiv
        Advances in Mathematics, 329, (2018), 273-328.

The paper in which we introduced the intermediate dimensions is here:

► Intermediate dimensions (with K. J. Falconer & T. Kempton), arXiv
        Mathematische Zeitschrift, 296, (2020), 813-830.

The paper in which we introduced the Fourier spectrum is here:

► The Fourier spectrum and sumset type problems, arXiv
        Mathematische Annalen (to appear).

I developed a discrete analogue of the Fourier spectrum in the setting of vector spaces over finite fields here:

► L^p averages of the Fourier transform in finite fields, arXiv
        submitted.

Other work on these notions include the following:

► A new perspective on the Sullivan dictionary via Assouad type dimensions and spectra (with L. Stuart), arXiv
        Bulletin of the American Mathematical Society (to appear).

► The fractal structure of elliptical polynomial spirals (with S. A. Burrell and K. J. Falconer), arXiv
        Monatshefte für Mathematik, 199, (2022), 1-22.

► Projection theorems for intermediate dimensions (S. A. Burrell & K. J. Falconer), arXiv
        Journal of Fractal Geometry, 8, (2021), 95-116.

► The Assouad spectrum and the quasi-Assouad dimension: a tale of two spectra (with K. E. Hare, K. G. Hare, S. Troscheit & H. Yu), arXiv
        Annales Academiæ Scientiarum Fennicæ Mathematica, 44, (2019), 379-387.

► Assouad type spectra for some fractal families (with H. Yu), arXiv
        Indiana University Mathematics Journal, 67, (2018), 2005-2043.

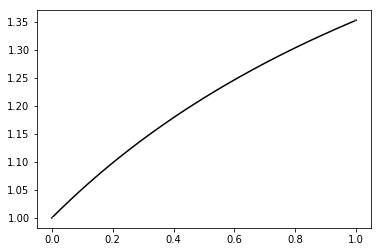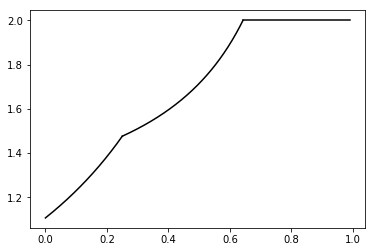
Plots of the Assouad spectrum (left) and intermediate dimensions (right) for an elliptical polynomial spiral. The Assouad spectrum typically has an increasing part and then a constant part, and the phase transition between these two regimes often has particular geometric significance. The smaller phase transition typically does not appear and was a surprise observation for this family of set.